一、前言

机器学习并不全是神经网络，相当多的机器学习算法都非常简单和直观，一个一个慢慢学。先学习一个最基本的分类（Classification）和回归（Regression）算法：KNN(k-nearest neighbor) 算法。

一句话来概括：人以类聚，物以群分。属于有监督学习。

举个栗子，我们去买水果，为什么我们能从一些特征（Feature）中分类出橘子和橙子（比如重量，软硬，表皮的褶皱，颜色的深浅）？因为同一类数据之间的特征更为相似，而不同种类数据之间的特征差别更大，那么如何用数学或者模型来判断什么叫相似，什么叫差别更大？

二、KNN算法的原理

在分类任务中，我们的目标是判断$x$的类别$y$。KNN会先观察与该样本点距离最近的$K$个样本，统计这些样本所属的类别，判断哪一类出现的次数最多，然后将该样本归类到次数最多的类中。

举个栗子：如图1 所示，假设现在有Class A 和Class B以及还未分类的红色五角星。目标任务是判断当前红色五角星属于哪个类别？

按照思路：

• 当K = 3时，Class B的数量大于Class A，因此红色五角星应该判定为属于Class B。
• 当K = 6时，Class A的数量大于Class B，因此红色五角星应该判定为属于Class A。

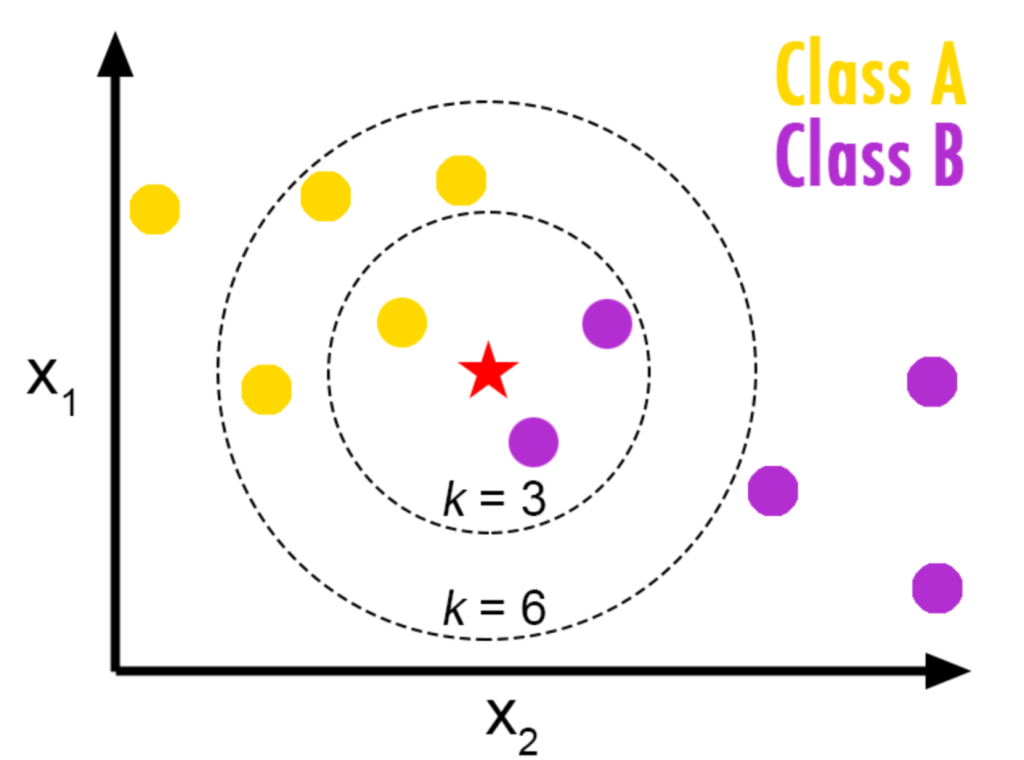
从这个例子可以看出KNN的基本思路是让当前样本的分类服从邻居中的多数分类。但是，当K的大小变化时，由于邻居数量的变化，其多少类别也会跟着发生变化，从而影响到对当前样本的分类判断。

因此，决定K的大小是KNN最重要的部分之一。当K的取值太小，分类结果很容易受到样本周围个别噪声数据的影响，容易发生过拟合；当K取的太大，又可能将远处一些不相干的样本数据包含进来，容易发生欠拟合，那么如何来确定K值呢？以及如何度量这个距离？

重要参数的确定：

1. K 值
2. 距离度量

三、选择K值

确定K值的方法有：

1. 交叉验证法：

原理：将数据集划分为多个子集，在每次验证过程中，选一个子集作为验证集，其余子集作为训练集，对于不同的K值进行模型训练和评估，最后计算每个K值在所有验证集上的平均性能，选性能最优的K值（就是尝试多个不同的K值，并通过在验证集上的表现（如准确率、F1分数等）来选择表现最好的 K 值）。

案例：（鸢尾花数据集YYDS）

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
import numpy as np

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 定义K值的范围
k_range = range(1, 31)
k_scores = []

# 对每个K值进行交叉验证
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X, y, cv=5, scoring='accuracy')
    k_scores.append(scores.mean())

# 找到最佳K值
best_k = np.argmax(k_scores) + 1
print(f"最佳K值为: {best_k}")

2. 网格搜索法

原理：该方法会在一个预先设定好的 K 值范围内，对每个可能的 K 值进行尝试，使用交叉验证来评估模型在不同 K 值下的性能，最终选取性能最优的 K 值。

案例：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 定义K值的搜索范围
param_grid = {'n_neighbors': range(1, 21)}

# 创建KNN分类器
knn = KNeighborsClassifier()

# 使用网格搜索进行参数调优
grid_search = GridSearchCV(knn, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 输出最佳K值
best_k = grid_search.best_params_['n_neighbors']
print(f"最佳K值为: {best_k}")

3. 经验法，加权平均等等

四、度量距离

在 KNN（K – 最近邻）算法中，距离的确定至关重要，它用于衡量数据点之间的相似性，进而找出待预测点的 K 个最近邻。以下是几种常见的距离度量算法：

1. 欧式距离（Euclidean Distance）

定义：欧氏距离是最常用的距离度量方法之一，它基于勾股定理，用于计算 n 维空间中两个点之间的直线距离。

公式：对于两个 n 维向量$\vec{x} = (x_1,x_2,\cdots,x_n)$和$\vec{y} = (y_1,y_2,\cdots,y_n)$，那他们之间的欧式距离$d(\vec{x},\vec{y})$ 为：

$$d(\vec{x},\vec{y}) = \sqrt{\sum_{i = 1}^{n}(x_i – y_i)^2}$$

案例：

import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

distance = np.sqrt(np.sum((x - y) ** 2))
print(f"欧氏距离: {distance}")

应用场景：适用于数据分布较为均匀、特征之间相互独立的情况，在很多实际问题中都有广泛应用，如地理坐标距离计算、图像像素相似度计算等。

2. 曼哈顿距离（Manhattan Distance）

定义：也称为城市街区距离，它是指在网格状的城市街道中，从一个点到另一个点沿着街道行走的最短距离（类似下围棋，只能x和y方向走网格点）。

公式：对于两个 n 维向量$\vec{x} = (x_1,x_2,\cdots,x_n)$和$\vec{y} = (y_1,y_2,\cdots,y_n)$，那他们之间的曼哈顿距离$d(\vec{x},\vec{y})$ 为：

$$d(\vec{x},\vec{y}) = \sum_{i = 1}^{n}|x_i – y_i|$$

案例：

import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

distance = np.sum(np.abs(x - y))
print(f"曼哈顿距离: {distance}")

3. 闵可夫斯基距离（Minkowski Distance）

定义：闵可夫斯基距离是欧氏距离和曼哈顿距离的推广，它引入了一个参数 p，通过改变 p 的值可以得到不同的距离度量。

公式：对于两个 n 维向量$\vec{x} = (x_1,x_2,\cdots,x_n)$和$\vec{y} = (y_1,y_2,\cdots,y_n)$，他们之间的闵可夫斯基距离$d(\vec{x},\vec{y})$ 为：

$$d(\vec{x},\vec{y}) = (\sum_{i = 1}^{n}(x_i – y_i)^p)^{1/p}$$

其中，$p>=1$。当$p = 2$时，闵可夫斯基距离就是欧氏距离；当$p = 1$时，就是曼哈顿距离。

案例：

import numpy as np
from scipy.spatial.distance import minkowski

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
p = 3

distance = minkowski(x, y, p)
print(f"闵可夫斯基距离 (p={p}): {distance}")

4. 切比雪夫距离（Chebyshev Distance）

定义：切比雪夫距离是指在 n 维空间中，两个点在各个坐标上的差值的最大值。

公式：对于两个 n 维向量$\vec{x} = (x_1,x_2,\cdots,x_n)$和$\vec{y} = (y_1,y_2,\cdots,y_n)$，他们之间的切比雪夫距离$d(\vec{x},\vec{y})$ 为：

$$d(\vec{x},\vec{y}) = \max_{i = 1}^{n}|x_i – y_i|$$

案例：

import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

distance = np.max(np.abs(x - y))
print(f"切比雪夫距离: {distance}")

5. 余弦相似度（Cosine Similarity）与余弦距离

定义：余弦相似度通过计算两个向量的夹角余弦值来衡量它们的方向相似度，值越接近 1 表示方向越相似。余弦距离则是用 1 减去余弦相似度得到，用于表示向量之间的差异程度。

公式：对于两个 n 维向量$\vec{x} = (x_1,x_2,\cdots,x_n)$和$\vec{y} = (y_1,y_2,\cdots,y_n)$，他们之间的余弦相似度距离$sim(\vec{x},\vec{y})$ 为：

$$sim(\vec{x},\vec{y}) = \frac{\mathbf{A}\cdot\mathbf{B}}{\|\mathbf{A}\|\|\mathbf{B}\|}=\frac{\sum_{i = 1}^{n}A_iB_i}{\sqrt{\sum_{i = 1}^{n}A_{i}^{2}}\sqrt{\sum_{i = 1}^{n}B_{i}^{2}}}$$

余弦距离 : $d(\vec{x},\vec{y}) = 1 – sim(\vec{x},\vec{y})$

案例：

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity

x = np.array([[1, 2, 3]])
y = np.array([[4, 5, 6]])

similarity = cosine_similarity(x, y)
distance = 1 - similarity[0][0]
print(f"余弦距离: {distance}")

应用场景：常用于文本挖掘、信息检索等领域，因为它更关注向量的方向而不是向量的长度，适合处理高维稀疏数据。

五、应用场景

1. 分类问题场景：

1.1 医疗诊断：

原理：根据患者的症状、检查结果等特征构建特征向量。对于一个新患者，找到与他特征最相似的 K 个患者，根据这 K 个患者的诊断结果来推断新患者可能患有的疾病。

示例：根据患者的体温、血压、血液指标等信息，使用 KNN 算法辅助医生判断患者是否患有某种疾病，如糖尿病、心脏病等。

1.2 商品推荐

原理：根据用户的历史购买记录、浏览行为、评价信息等构建用户的特征向量。对于一个用户，找到与他兴趣最相似的 K 个用户，根据这 K 个用户购买过的商品来为该用户推荐商品。

示例：电商平台根据用户的购物历史和偏好，使用 KNN 算法为用户推荐可能感兴趣的商品，提高用户的购买转化率和满意度。

2. 回归问题场景

2.1 房价预测

原理：将房屋的各种特征（如面积、房间数量、房龄、地理位置等）作为特征向量。对于一个待预测房价的房屋，找到与它特征最相似的 K 个房屋，计算这 K 个房屋的平均房价或加权平均房价，将其作为待预测房屋的房价。

示例：在房地产市场中，通过收集大量房屋的相关信息和实际成交价格，使用 KNN 算法可以为新上市的房屋提供合理的价格预测。

2.2 股票价格预测

原理：选取股票的历史价格、成交量、市盈率等特征构建特征向量。对于未来某一时刻的股票价格预测，找到与当前时刻特征最相似的 K 个历史时刻，根据这 K 个时刻之后的股票价格变化情况来预测未来的股票价格。

示例：投资者可以利用 KNN 算法结合股票的历史数据，对股票的未来走势进行预测，辅助投资决策。

六、实战案例

1. KNN 分类（iris数据集）

鸢尾花数据集是一个非常经典且常用的数据集，包括150个样本，属于多分类问题的数据集。

特征：该数据集主要有 4 个数值型特征，用于描述鸢尾花的物理特征。

• 萼片长度（sepal length）：单位为厘米，指鸢尾花萼片的长度。
• 萼片宽度（sepal width）：单位为厘米，即鸢尾花萼片的宽度。
• 花瓣长度（petal length）：单位为厘米，是鸢尾花花瓣的长度。
• 花瓣宽度（petal width）：单位为厘米，也就是鸢尾花花瓣的宽度。

标签：样本被分为 3 个不同的类别，代表 3 种不同种类的鸢尾花。

• 山鸢尾（Iris-setosa）
• 变色鸢尾（Iris-versicolor）
• 维吉尼亚鸢尾（Iris-virginica）

案例：直接用sklearn 导入iris数据集

from sklearn.datasets import load_iris

iris = load_iris()

x = iris.data

y = iris.target

feature_names = iris.feature_names

target_names = iris.target_names

数据结果：

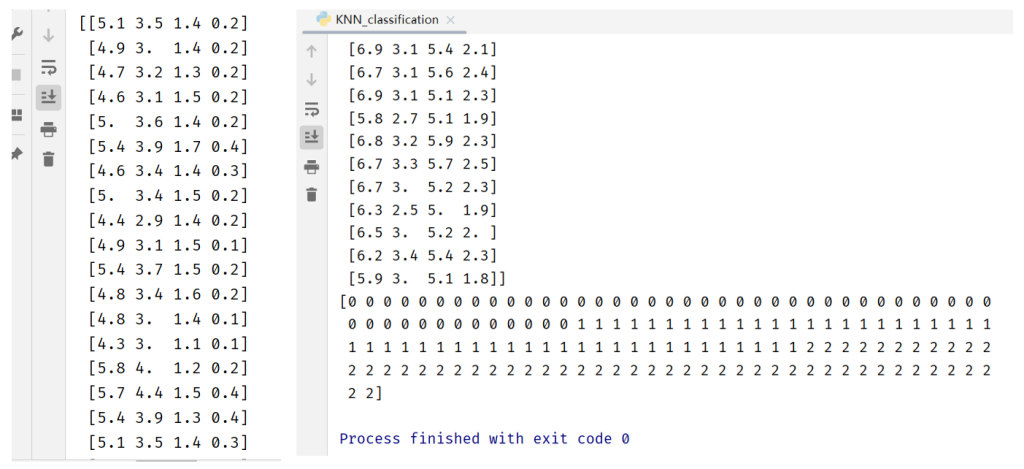
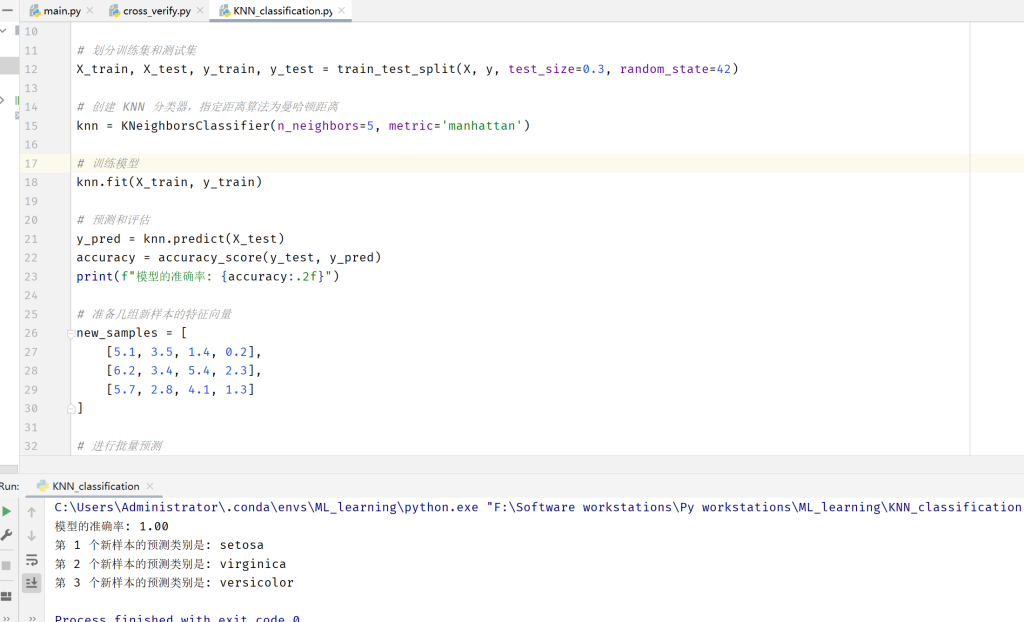
要求：使用iris数据集，结合KNN算法（使用曼哈顿距离算法）进行鸢尾花的分类；生成好模型之后，随机给几组特征向量，来检查分类情况。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
iris = load_iris()
X = iris.data  # 特征数据
y = iris.target  # 标签数据

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建 KNN 分类器，指定距离算法为曼哈顿距离
knn = KNeighborsClassifier(n_neighbors=5, metric='manhattan')

# 训练模型
knn.fit(X_train, y_train)

# 预测和评估
y_pred = knn.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"模型的准确率: {accuracy:.2f}")

# 准备几组新样本的特征向量
new_samples = [
    [5.1, 3.5, 1.4, 0.2],
    [6.2, 3.4, 5.4, 2.3],
    [5.7, 2.8, 4.1, 1.3]
]

# 进行批量预测
predicted_classes = knn.predict(new_samples)
target_names = iris.target_names

# 输出每个样本的预测类别名称
for i, predicted_class in enumerate(predicted_classes):
    predicted_class_name = target_names[predicted_class]
    print(f"第 {i + 1} 个新样本的预测类别是: {predicted_class_name}")

结果为：

2. KNN回归预测（糖尿病数据集）